Kunci Jawaban Matematika Kelas 9 Halaman 303 - 305 Latihan 5.3

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 9 Semester 1 Halaman 303 - 305. Bab 5 Bangun Ruang Sisi Lengkung Latihan 5.3 Hal 303 - 305 Nomor 1 - 10 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 9 di semester 1 halaman 303 - 305. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 9 dapat menyelesaikan tugas Bangun Ruang Sisi Lengkung Kelas 9 Halaman 303 - 305 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 9 Semester 1.

Kunci Jawaban Matematika Kelas 9 Halaman 303 - 305 Latihan 5.3

1. Tentukan luas permukaan dan volume bangun bola berikut.

Jawaban :

Volume bola = 4/3 x π × r³
Luas permukaan bola = 4 × π × r²

a) Luas = 4 x π x 12 x 12
= 576π m²
Volume = 4/3 x π x 12 x 12 x 12
= 2304π m³

b) Luas = 4 x π x 5 x 5
= 100π cm²
Volume = 4/3 x π x 5 x 5 x 5
= 500/3π cm³

c) Luas = 4 x π x 6 x 6
= 144π dm²
Volume = 4/3 x π x 6 x 6 x 6
= 288π dm³

d) Luas = 4 x π x 4,5 x 4,5
= 81π cm²
Volume = 4/3 x π x 4,5 x 4,5 x 4,5
= 243/2π cm³

e) Luas = 4 x π x 10 x 10
= 400π m²
Volume = 4/3 x π x 10 x 10 x 10
= 4000/3π m³

f) Luas = 4 x π x 15 x 15
= 900π m²
Volume = 4/3 x π x 15 x 15 x 15
= 4500π m³

2. Berapakah luas permukaan bangun setengah bola tertutup berikut.

Jawaban :

Volume setengah bola = (4/3 x π × r³) / 2
Luas permukaan setengah bola = (4 × π × r²) / 2 + (π × r²)

a) Luas = 48π cm²
Volume = 128/3π cm³

b) Luas = 432π cm²
Volume = 1.152π cm³

c) Luas = 108π cm²
Volume = 144π cm³

d) Luas = 192π m²
Volume = 1.024/3π m³

e) Luas = 675/4π m²
Volume = 1.125/4π m³

f) Luas = 363π dm²
Volume = 2.662/3π dm³

3. Dari soal-soal nomor 2 tentukan rumus untuk menghitung luas permukaan setengah bola tertutup.

Jawaban : 

Luas permukaan stengah bola = (luas permukaan bola)/2 + luas lingkaran 
= (4πr²)/2 + πr²
= 3πr²

4. Tentukan jari-jari dari bola dan setengah bola tertutup berikut.

Jawaban :

a) L = 4 × π × r²
729π = 4 x π x r²
r = √(729/4
r = 27/2 cm

b) V = 4/3 x π × r³
2.304π = 4/3 x π x r³
r³ = 2.304 x 3/4
r = 12 cm

c) V = 4/3 x π × r³
36π = 4/3 x π x r³
r³ = 36 x 3/4
r = 3 cm

d) L = 3 × π × r²
27π = 4 x π x r²
r = √(27/3
r = 3 m

e) L = 3 × π × r²
45π = 3 x π x r²
r = √(45/3
r = √15 m

f) V = 2/3 x π × r³
128/3π = 2/3 x π x r³
r³ = 128/3 x 3/2
r = 4 m

5. Berpikir kritis.Terdapat suatu bola dengan jari-jari r cm. Jika luas permukaan bola tersebut adalah A cm2 dan volume bola tersebut adalah A cm3, tentukan:

Jawaban :

a) Luas permukaan = 4πr² 
Volume = 4/3 πr³ 
4πr² = 4/3 πr³ 
r = 3 cm
Jadi, nilai r adalah 3 cm.

b) Luas permukaan = 4πr² 
= 4π(3)² 
= 36π
Jadi, nilai A adalah 36π.

6. Bangun di samping dibentuk dari dua setengah bola yang sepusat. Setengah bola yang lebih kecil memiliki jari-jari r1 = 4 cm sedangkan yang lebih besar memiliki jari-jari r2 = 8 cm.

Jawaban :

7. Analisis kesalahan. Lia menghitung luas permukaan bola dengan cara membagi volume bola dengan jari-jari bola tersebut (L = V/r).

Jawaban : 

L = 4πr², V = 4/3 πr³. 
Sehingga V = Lr/3, yang berakibat L = 3V/r

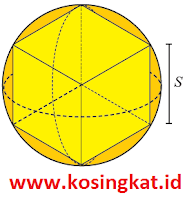
8. Bola di dalam kubus. Terdapat suatu kubus dengan panjang sisi s cm. Dalam kubus tersebut terdapat bola dengan kondisi semua sisi kubus menyentuh bola (lihat gambar di samping).

Jawaban :

Karena semua sisi kubus menyentuh bola maka diameter bola = s, jari-jari bola = s/2

a) Luas permukaan bola =  4 × π × r²
= 4 x π x s/2 x s/2
=  πs² cm²

b) Volume bola = 4/3 x π × r³
= 4/3 x π x s/2 x s/2 x s/2
= πs³/6 cm³

9. Kubus di dalam bola. Terdapat suatu kubus dengan panjang sisi s cm. Kubus tersebut berada di dalam bola dengan kondisi semua titik sudut kubus menyentuh bola.

Jawaban :

Diagonal bidang kubus = diameter bola, diperoleh r = 1/2√3s

a) Luas = 4πr² 
= 4π(1/2√3s)²
= 3πs² cm²

b) Volume = 4/3πr³
= 4/3π(1/2√3s)³
= 1/2√3πs³ cm³

10. Timbangan dan kelereng. Andi punya dua macam kelereng. Kelereng tipe I berjari-jari 2 cm sedangkan tipe II berjari-jari 4 cm.

Jawaban :

Misalkan banyaknya kelereng tipe I adalah m sedangkan tipe II adalah n.

V1 = 4/3π(2)³ = 32/3π cm 
V2 = 4/3π(4)³ = 256/3π cm 

m x V1 = n x V2π
m x 32/3π = n x 256/3π
m = 8n

Jadi, perbandingan banyak kelereng pada sisi kiri dengan sisi kanan agar seimbang adalah  8 : 1.

Bagikan Artikel ini