Kunci Jawaban Matematika Kelas 7 Halaman 244 Ayo Kita Berlatih 8.4

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman  244. Bab 8 Segiempat dan Segitiga Ayo Kita berlatih 8.4 Hal  244 Nomor 9, 10, 11, 12, 13, 14, 15. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 7 di semester 2 halaman  244. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 7 dapat menyelesaikan tugas Segiempat dan Segitiga Matematika Kelas 7 Halaman  244 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 7 Semester 2.

Daftar Isi Kunci Jawaban Ayo Kita Berlatih 8.4 :

• Baca Juga : Kunci Jawaban Halaman 242 Nomor 1 - 5
• Baca Juga : Kunci Jawaban Halaman 243 Nomor 6 - 8
• Baca Juga : Kunci Jawaban Halaman 244 Nomor 9 - 15

Kunci Jawaban Matematika Kelas 7 Halaman 244 Ayo Kita Berlatih 8.4

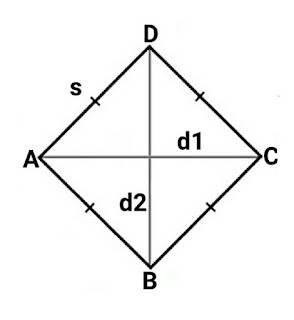
9. Diketahui jajargenjang ABCD. Titik P dan Q terletak pada AC sehingga DP dan BQ tegak lurus AC. Jika panjang AD = 13 cm, AC = 25 cm dan luas jajargenjang tersebut adalah 125 cm2, maka panjang PQ adalah ... cm

a. 1/2 

b. 1 

c. 2

d. 3 

e. 4/3

Jawaban :

*Perhatikan ilustrasi gambar diatas*

Luas jajargenjang ABCD = 2 x luas segitiga ACD
Luas jajargenjang ABCD = 2 x ( alas x DP / 2 )
125 = 2 x ( 25 x DP / 2)
125 = 25 DP
DP = 125 / 25
DP = 5 cm

AP² = AD² - DP²
AP =  √(AD² - DP²)
= √(13² - 5² )
= √( 169 - 25 )
= √144
= 12 cm

PQ = AC - ( 2 x AP )
= 25 - ( 2 x 12 )
= 25 - 24
= 1 cm

Jadi, panjang PQ adalah b.1 cm.

10. Diketahui luas suatu trapesium adalah 60 cm2. Jika hasil pembagian panjang sisi-sisi sejajarnya adalah 3/5 cm, dan tinggi trapesium 15 cm, tentukan panjang masing-masing sisi sejajar tersebut.

Jawaban :

X/Y = 3/5

X = 3Y/5

Luas Trapesium = 1/2 x ( jumlah sisi sejajar ) x tinggi

60 = 1/2 x ( X + Y ) x 15

60 = 1/2 x ( 3Y/5 + Y ) x 15

60 x 2 / 15 = 8Y/5

8 = 8Y/5

8Y = 8 x 5

Y = 40 / 8

Y = 5 cm

X = 3Y/5

X = ( 3 x 5 ) / 5

X = 3 cm

Jadi, panjang masing-masing sisi sejajar tersebut adalah 3 cm dan 5 cm.

11. Diketahui jajar genjang ABCD dengan titik E dan F merupakan titik tengah garis AB dan CD. Tarik garis AF, BF, DE, dan CE. Bentuk segiempat apakah yang terbentuk ditengah-tengah jajar genjang tersebut? Jelaskan jawabanmu!

Jawaban :

Jadi, bentuk segiempat yang terbentuk ditengah-tengah jajar genjang tersebut adalah Jajargenjang. Karena memiliki diagonal yang sama panjang dan saling berpotongan tidak tegak lurus.

12. Diketahui jajargenjang ABCD. Titik P dan Q terletak pada AC sehingga DP dan BQ tegak lurus AC. Jika panjang AD = 13 cm, AC = 25 cm dan luas jajargenjang tersebut adalah 125 cm2, maka panjang PQ adalah ... cm

Jawaban :

*Perhatikan ilustrasi gambar diatas*

Luas jajargenjang ABCD = 2 x luas segitiga ACD
Luas jajargenjang ABCD = 2 x ( alas x DP / 2 )
125 = 2 x ( 25 x DP / 2)
125 = 25 DP
DP = 125 / 25
DP = 5 cm

AP² = AD² - DP²
AP =  √(AD² - DP²)
= √(13² - 5² )
= √( 169 - 25 )
= √144
= 12 cm

PQ = AC - ( 2 x AP )
= 25 - ( 2 x 12 )
= 25 - 24
= 1 cm

Jadi, panjang PQ adalah 1 cm.

13. Diketahui panjang salah satu diagonal belahketupat 48 cm. Bila keliling belahketupat 100 cm, maka tentukan luas belahketupat tersebut.

Jawaban : 

Diagonal 1 = 48 cm

Keliling = 100 cm

4 x S = 100 cm

S = 100/4

S = 25 cm

Diagonal 2 =  √(S² - ( 1/2 x Diagonal 1)²)

= √(25² - ( 1/2 x 48)²)

= √(625 - 576)

= √49

= 7 cm

Luas belah ketupat = 1/2 x Diagonal 1 x Diagonal 2

= 1/2 x 48 x 7

= 336 cm²

Jadi, luas belah ketupat tersebut adalah 336 cm².

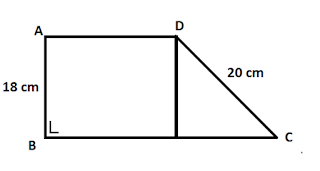
14. Diketahui trapesium ABCD siku-siku di B dengan panjang AB = 18 cm, CD = 20 cm, dan luasnya 108 cm2. Hitunglah keliling trapesium ABCD tersebut.

Jawaban :

Luas trapesium = 1/2 x ( jumlah sisi sejajar) x tinggi

108 = 1/2 x  ( jumlah sisi sejajar) x 18

( jumlah sisi sejajar) = 108 x 2 / 18

( jumlah sisi sejajar) = 12 cm

Keliling = ( jumlah sisi sejajar ) + tinggi + DC

= 12 + 18 + 20

= 50 cm

Jadi, keliling trapesium ABCD tersebut adalah 50 cm.

15. Diketahui ABCD dan CEGH adalah dua persegipanjang kongruen dengan panjang 17 cm, dan lebar 8 cm. Titik F adalah titik potong sisi AD dan EG. Tentukan luas segiempat EFDC !

Jawaban :

Untuk mencari panjang CL dapat menggunakan rumus pythagoras dengan EL sebagai tinggi dan CE sebagai sisi miring.
CL = √(17² - 8²
= √225
= 15 cm

 Misal X adalah AF,
FD = FE maka
(8 - X)² = 2² + X²
64 - 16X + X² = 4 + X²
60 = 16X
X = 15/4
X = 3,75

FD = 8 - 3,75
FD = 4,25

Perhatikan bangun EFDC, bangun EFDC merupakan bangun layang layang sehingga,
luas segiempat EFDC = luas layang layang = 2 x luas segitiga CDF

Luas segiempat EFDC = 2 x ( 17 x 4,25 / 2 )
= 17 x 4,25
= 72,25 cm²

Jadi, luas segiempat EFDC adalah 72,25 cm².

Bagikan Artikel ini