Kunci Jawaban Matematika Kelas 9 Halaman 126 - 128 Latihan 2.5
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 9 Semester 1 Halaman 126 - 128. Bab 2 Persamaan dan Fungsi Kuadrat Latihan 2.5 Hal 126 - 128 Nomor 1 - 9 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 9 di semester 1 halaman 126 - 128. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 9 dapat menyelesaikan tugas Persamaan dan Fungsi Kuadrat Kelas 9 Halaman 126 - 128 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 9 Semester 1.
4. Sebuah peluru ditembakkan vertikal ke atas. Tinggi peluru h (dalam meter) sebagai fungsi waktu t (dalam detik) dirumuskan dengan h(t) = –4t2 + 40t.
Kunci Jawaban Matematika Kelas 9 Halaman 126 - 128 Latihan 2.5
1. Suatu persegi panjang kelilingnya 60 cm. Tentukan ukuran persegi panjang agar mempunyai luas maksimum.
Jawaban :
Keliling = 2 x (panjang + lebar)
30 = p + l
p = 30 - l
luas = p x l = (30 - l) x l = 30l - l2
l = -b / 2(a)
= -30 / 2(-1)
= 15
p = 30 - l
= 30 - 15
= 15
Jadi, ukuran persegi panjang tersebut agar mempunyai luas maksimum adalah lebar = 15 cm dan panjang = 15 cm.
Keliling = 2 x (panjang + lebar)
30 = p + l
p = 30 - l
luas = p x l = (30 - l) x l = 30l - l2
l = -b / 2(a)
= -30 / 2(-1)
= 15
p = 30 - l
= 30 - 15
= 15
Jadi, ukuran persegi panjang tersebut agar mempunyai luas maksimum adalah lebar = 15 cm dan panjang = 15 cm.
2. Sebuah segitiga siku-siku jumlah kedua sisi siku-sikunya adalah 50 cm. Tentukan ukuran segitiga siku-siku agar mempunyai luas maksimum.
Jawaban :
Misal a = alas, b = tinggi, dan c = sisi miring
a + b = 50
a = 50 - b
Luas = 1/2 x a x b
L(b) = 1/2 x (50 - b)(b)
L(b) = 25b - 1/2b²
Maksimum jika L'(b) = 0
25 - b = 0
b = 25
a + b = 50
a + 25 = 50
a = 25
c = √a2 + b2
= √252 + 252
= 25√2
Jadi, ukuran segitga siku-siku tersebut agar mempunyai luas maksimum adalah 25 cm x 25 cm x 25√2.
Misal a = alas, b = tinggi, dan c = sisi miring
a + b = 50
a = 50 - b
Luas = 1/2 x a x b
L(b) = 1/2 x (50 - b)(b)
L(b) = 25b - 1/2b²
Maksimum jika L'(b) = 0
25 - b = 0
b = 25
a + b = 50
a + 25 = 50
a = 25
c = √a2 + b2
= √252 + 252
= 25√2
Jadi, ukuran segitga siku-siku tersebut agar mempunyai luas maksimum adalah 25 cm x 25 cm x 25√2.
3. Seorang siswa memotong selembar kain. Kain hasil potongannya berbentuk persegi panjang dengan keliling 80 cm.
Jawaban :
Keliling = 2 x (panjang + lebar)
80 = 2 x (p + l)
40 = p + l
p = 40 - l
L(l) = p x l
= (40 - l) x l
= 40l - l2
Karena luas maksimum maka,
l = - b/2a
= - 40 / 2(-1)
= - 40 / -2
= 20 cm
p = 40 - l
= 40 - 20
= 20
Jadi, untuk mendapatkan potongan yang mempunyai luas maksimum maka panjang dan lebar kainnya adalah p = 20 dan l = 20.
Keliling = 2 x (panjang + lebar)
80 = 2 x (p + l)
40 = p + l
p = 40 - l
L(l) = p x l
= (40 - l) x l
= 40l - l2
Karena luas maksimum maka,
l = - b/2a
= - 40 / 2(-1)
= - 40 / -2
= 20 cm
p = 40 - l
= 40 - 20
= 20
Jadi, untuk mendapatkan potongan yang mempunyai luas maksimum maka panjang dan lebar kainnya adalah p = 20 dan l = 20.
4. Sebuah peluru ditembakkan vertikal ke atas. Tinggi peluru h (dalam meter) sebagai fungsi waktu t (dalam detik) dirumuskan dengan h(t) = –4t2 + 40t.
Jawaban :
Waktu supaya tinggi maksimum adalah
t = - b / 2a
= - 40 / 2(-4)
= - 40 / - 8
= 5
Maka tinggi maksimumnya adalah,
h(t) = –4t2 + 40t
h(5) = –4(52) + 40(5)
= -100 + 200
= 100 meter
Jadi, tinggi maksimum yang dapat dicapai peluru dan waktu yang diperlukan adalah t = 5 detik dan h = 100 meter.
Waktu supaya tinggi maksimum adalah
t = - b / 2a
= - 40 / 2(-4)
= - 40 / - 8
= 5
Maka tinggi maksimumnya adalah,
h(t) = –4t2 + 40t
h(5) = –4(52) + 40(5)
= -100 + 200
= 100 meter
Jadi, tinggi maksimum yang dapat dicapai peluru dan waktu yang diperlukan adalah t = 5 detik dan h = 100 meter.
5. Diketahui bahwa tinggi Jam Gadang yang ada di Sumatera adalah 26 meter.
Jawaban :
a) Gunakan persamaan s = s0 – v0t + 5t2 dengan subtitusi s0 = tinggi jam gadang = 26, s = 0 dan t = 0,7 sehingga didapat
0 = 26 – v0 (0,7) + 5(0,49)
Dengan demikian
v0 = (26 + 2,45) / 0,7
= 28,45 / 0,7
= 40,643
b) Gunakan persamaan h = h0 + v0t – 5t2 dengan subtitusi h0 = 0, dengan demikian tinggi maksimum adalah
ymaksimum = - D / 4a
= - (b2 - 4ac) / 4a
= - (v0 - 4 (-5)(0)) / 4(-5)
= v02 / 20
Dan subtitusi ymaksimum = 26 maka didapat
v0= ± 520
Karena kecepatan harus bernilai positif maka
v0 = 520
a) Gunakan persamaan s = s0 – v0t + 5t2 dengan subtitusi s0 = tinggi jam gadang = 26, s = 0 dan t = 0,7 sehingga didapat
0 = 26 – v0 (0,7) + 5(0,49)
Dengan demikian
v0 = (26 + 2,45) / 0,7
= 28,45 / 0,7
= 40,643
b) Gunakan persamaan h = h0 + v0t – 5t2 dengan subtitusi h0 = 0, dengan demikian tinggi maksimum adalah
ymaksimum = - D / 4a
= - (b2 - 4ac) / 4a
= - (v0 - 4 (-5)(0)) / 4(-5)
= v02 / 20
Dan subtitusi ymaksimum = 26 maka didapat
v0= ± 520
Karena kecepatan harus bernilai positif maka
v0 = 520
6. Seorang pemain bola basket mempunyai tinggi 170 cm. Sedangkan tinggi keranjang adalah 3 meter.
Jawaban : Lemparan tersebut tidak akan masuk ke dalam keranjang.
7. Seorang tukang bangunan mendapat pesanan membuat air mancur yang diletakkan di pusat kolam kecil yang berbentuk lingkaran.
8. Seorang atlet lompat jauh sedang mengadakan latihan. Pada saat latihan dia mengambil awalan lari dengan kecepatan tertentu dan pada saat di balok tumpuan kecepatannya kira-kira 2.5 m/s kemudian pada saat itu juga dia melompat dengan sudut 300.
Jawaban :
Pada saat orang tersebut ditanah,
1/2 v0t - 5t2 = 0
Dengan demikian,
t = 0 atau t = 0,25
Sehingga,
s = 1/2√3 x 2,5 x 0,25
= 0,3125√3
= 0,5413
Jadi, jarak atlet tersebut dengan balok tumpuan ketika dia sampai di tanah adalah 0,5413 meter.
Pada saat orang tersebut ditanah,
1/2 v0t - 5t2 = 0
Dengan demikian,
t = 0 atau t = 0,25
Sehingga,
s = 1/2√3 x 2,5 x 0,25
= 0,3125√3
= 0,5413
Jadi, jarak atlet tersebut dengan balok tumpuan ketika dia sampai di tanah adalah 0,5413 meter.
9. Seorang atlet lompat tinggi sedang mengadakan latihan. Pada saat latihan dia mengambil awalan lari dengan kecepatan tertentu dan dia melompat dengan sudut mendekati 90° pada saat jaraknya sangat dekat sekali dengan tiang lompat.

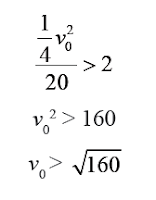
2 Komentar untuk "Kunci Jawaban Matematika Kelas 9 Halaman 126 - 128 Latihan 2.5"
no 5 yg a salah
oke terima kasih atas infonya jawaban no 5 a sudah diperbaiki ya :)
Posting Komentar