Kunci Jawaban Matematika Kelas 8 Halaman 200 - 202 Ayo Kita Berlatih 8.7

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 200 - 202. Bab 8 Bangun Ruang Sisi Datar Ayo Kita berlatih 8.7  Hal 200 - 202 Nomor 1, 2, 3, 4, 5, 6. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 200 - 202. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Bangun Ruang Sisi Datar Kelas 8 Halaman 200 - 202 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.

Kunci Jawaban Matematika Kelas 8 Halaman 200 - 202 Ayo Kita Berlatih 8.7

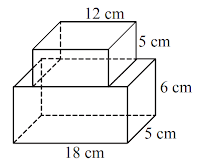
1. Perhatikan gambar di bawah. 18 cm 5 cm 5 cm 12 cm 6 cm Tentukan luas permukaan dan volumenya.

Jawaban :

Luas permukaan balok I = 2 x ((p x l) + (p x t) + (l x t) )
= 2 x ((18 x 5) + (18 x 6) + (5 x 6) )
= 2 x (90 + 108 + 30)
= 2 x 228
= 456 cm²


Luas permukaan balok II = 2 x ((p x l) + (p x t) + (l x t) )
= 2 x ((12 x 5) + (12 x 5) + (5 x 5) )
= 2 x (60 + 60 + 25)
= 2 x 145
= 290 cm²

Luas persegi berhimpit = p x l
= 12 x 5
= 60 cm²

Luas permukaan seluruhnya = Luas balok I + Luas balok II - ( 2 x luas berhimpit)
= 456 + 290 - ( 2 x 60 )
= 746 - 120
= 626  cm²

Vbalok I = p x l x t
= 18 x 6 x 5
= 540  cm³

Vbalok II = p x l x t
= 12 x 5 x 5
= 300  cm³

Vbalok seluruhnya = Vbalok I + Vbalok II
= 540 + 300
= 840  cm³

Jadi, luas permukaannya adalah 626  cm² dan volumenya adalah 840 cm³.

2. Perhatikan gambar rangka bangun di samping. Rangka bangun tersebut terdiri atas dua bagian, yaitu balok dan limas.

Tentukan: 
a. luas permukaan balok. 
b. volume balok. 
c. luas alas limas. 
d. panjang diagonal alas limas. 
e. volume limas.

Jawaban :

a)
Luas permukaan balok = 5 x s x s
= 5 x 8 x 8
= 320 cm²

b)
Vbalok = s x s x s
= 8 x 8 x 8
= 512  cm²

c)
Luas alas limas = panjang EF x panjang FG
= 8 x 8
= 64  cm²

d)
Panjang diagonal alas = √(s² + s²)
= √(8² + 8²)
= √(64 + 64)
= 8√2
= 11,31 cm²

e)
Tinggi limas = (TG² - (1/2 x EG)²)
= √(8² - (1/2 x 8√2)²)
= √(64 - 32)
= √32
= 4√2
= 5,65 cm²

Vlimas = 1/3 x luas alas x tinggi
= 1/3 x 8 x 8 x 4√2
= 120,67 cm³

3. Sebuah tenda berbentuk bangun seperti berikut. Berapakah luas kain yang digunakan untuk membuat sebuah tenda seperti itu, bila alasnya berbentuk persegi dengan ukuran (4 × 4) m2 , tinggi bagian tenda yang berbentuk prisma 2 m dan tinggi sisi tegak bagian atapnya 3 m?

Jawaban :

Luas kain = luas selimut balok + luas sisi tegak pada limas
= (4 x s x t) + (4 x 1/2 x s x tinggi sisi tegak)
= (4 x 4 x 2) + (4 x 1/2 x 4 x 3)
= 32 + 24
= 56 m²

Jadi, luas kain yang digunakan untuk membuat tenda seperti itu adalah 56 m².

4. Ambillah enam benda-benda nyata yang ada di sekitar kalian, kemudian ukurlah dan perkirakan luas permukaan dan volumenya.

Jawaban :

Bangun 1) Penghapus
Panjang = 3cm, lebar = 1cm, tinggi = 1cm
Luas permukaan = 2 x (pl + pt + lt)
= 2 x ((3x1) + (3x1) + (1x1)
= 2 x 7
= 14 cm²
Volume = p x l x t
= 3 x 1 x 1
= 3 cm³

Bangun 2) Balok Kayu
Panjang = 100cm, lebar = 20cm, tinggi = 25cm
Luas permukaan = 2 x (pl + pt + lt)
= 2 x ((100x20) + (100x25) + (20x25)
= 2 x 5.000
= 10.000 cm²
Volume = p x l x t
= 100 x 20 x 25
= 50.000 cm³

Bangun 3) Sarang Buruk Kubus
Panjang = 30cm, lebar = 30cm, tinggi = 30cm
Luas permukaan = 2 x (pl + pt + lt)
= 2 x ((30x30) + (30x30) + (30x30)
= 2 x 2.700
= 5.400 cm²
Volume = p x l x t
= 30 x 30 x 30
= 9.000 cm³

Bangun 4) Toples Tabung
jari - jari = 7cm, tinggi = 20cm
Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)
= (2 x pi x r x r ) + (pi x diameter x tinggi)
= (2 x 22/7 x 7 x 7) + (22/7 x 2 x 7 x 20)
= 308 + 880
= 1.188 cm²
Volume = luas alas x tinggi
= pi x r x r x t
= 22/7 x 7 x 7 x 20
= 3.080 cm³

Bangun 5) Gelas
jari - jari = 3,5cm, tinggi = 10cm
Luas permukaan = (2 x luas alas) + (keliling alas x tinggi)
= (2 x pi x r x r ) + (pi x diameter x tinggi)
= (2 x 22/7 x 3,5 x 3,5) + (22/7 x 2 x 3,5 x 10)
= 77 + 220
= 297 cm²
Volume = luas alas x tinggi
= pi x r x r x t
= 22/7 x 3,5 x 3,5 x 10
= 385 cm³

Bangun 6) Akuarium Balok
Panjang = 100cm, lebar = 30cm, tinggi = 40cm
Luas permukaan = 2 x (pl + pt + lt)
= 2 x ((100x30) + (100x40) + (30x40)
= 2 x 8.200
= 16.400 cm²
Volume = p x l x t
= 100 x 30 x 40
= 120.000 cm³

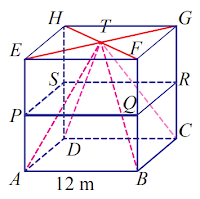
5. Perhatikan kubus ABCD.EFGH pada gambar berikut.

Titik A, B, C, dan D terletak pada bidang sisi bagian bawah. Titik T merupakan titik perpotongan garis diagonal pada bidang sisi bagian atas. Selanjutnya dibuat limas T.ABCD. Jika limas T.ABCD dipotong oleh bidang PQRS dimana titik P, Q, R, S, berturut terletak di tengah garis AE, BF, CG, dan DH. Jika dengan panjang rusuk kubus tersebut adalah 12 cm, maka tentukan volume limas terpancung bagian bawah.

Jawaban : 

Volume ABCD.VWXY = Volume T.ABCD - Volume T.VWXY

= (1/3 × AB × BC × TO) - (1/3 × VW × WX × TZ)

= (1/3 × 12 × 12 × 12)  - (1/3 × 6 × 6 × 6) 

= 576 - 72

= 504 cm³

Jadi, volume limas  terpancung bagian bawah adalah = 504 cm³.

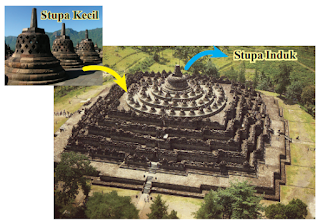
6. Bangunan Candi Borobudur terdiri atas tiga tingkatan, yaitu Kamadhatu, Rupadhatu, dan Arupadhatu. Arupadhatu merupakan bagian teratas candi yang denah lantainya berbentuk lingkaran. Di atas lantai ini terdapat sejumlah stupa kecil berbentuk lonceng yang disusun dalam tiga teras lingkaran melingkari stupa induk seperti yang ditunjukkan pada gambar berikut. 

Stupa Kecil Stupa Induk Pikirkan berapa banyak stupa kecil pada bagian Arupadhatu tersebut? Tuliskan strategimu.

Jawaban :

Strategi yang dilakukan adalah :
1. menghitung setengah sisi stupa kecil pada lingkaran terdalam.
2. mengalikan hasil setengah sisi stupa kecil pada lingkaran terdalam tadi dengan 2.
3. melakukan langkah 1 dan 2 yang sama hingga lingkaran ke-3. Lalu menjumlahkan seluruh stupa kecil pada tiap lingkaran.

Pada lingkaran pertama terdapat 12 buah.
Pada lingkaran kedua terdapat 24 buah
Pada lingkaran ketiga terdapat  36 buah
Total stupa kecil = 12 + 24 + 36
= 72 buah

Jadi, banyak stupa kecil pada bagian Arupadhatu adalah 72 buah.

Bagikan Artikel ini